In my last article, I covered a big chunk of the planning & discovery I did when building the first version of GuardianForge. As a quick recap, my backend at this phase of the project leveraged DynamoDB for storing information about builds, S3 for storing the JSON object that makes up a build, and Lightsail to host the API written in Go. In this one, I'm going to dive into more into detail with how I'm using DynamoDB.
Unless otherwise specified, code in this article should be considered "pseudo-code" and will likely not work in any specific language.
Accessing Data in DynamoDB
DynamoDB is a NoSQL solution in AWS. Its designed for scalability & performance, but structuring your data to properly take advantage of these capabilities is critical. Before I even considered how I wanted to store my data, I first needed to understand what I needed to store and how I wanted that data to be accessed. I started by creating a list of access patterns that I knew I would need;
- Get a single build.
- Get the latest N builds.
- Get all builds for a user.
- Get all builds that a user has saved.
- Get a user by their ID.
Understanding Keys
Just like every database system, there needs to be some way of uniquely identifying a record. In a traditional, relational SQL database, this would be the primary key. In Dynamo, you have two attributes which can be used to make up a unique identifier called the Partition Key (PK) and the Sort Key (SK). These together make up what's called a composite primary key, and as long as the combination are unique, it works.
Partition Key
Part of the way Dynamo achieves its performance & scalability goal is by storing data in "partitions" in AWS. As you'd expect, the PK is what determines how the data is partitioned.
Sort Key
The SK is used to perform queries on records within a partition, and only this field can be used to perform these queries. If you ever query data elements that are not specified in the SK, you're actually pulling all that data into your program and tossing out what doesn't match the query, which is pretty inefficient and should be avoided if possible. A way around this is using indexes, which I'll touch on in a bit.
The Sort Key has a number of operations that can be used when querying Dynamo;
- Equals
- Begins With
- Greater Than/GT Equal To
- Less Than/LT Equal To
- Between
SKs can also be used (as you'd imagine) to sort your data before it is returned to your program from Dynamo.
Before we get into how I decided to structure my data, I started with defining the base schema;
- PK:
entityType: string- The type of record it is. For builds, this will always be set tobuild. For users, this will beuser - SK:
entityId: string- A unique ID for the record. For builds, this will be a randomly generated GUID. For users, it is a unique integer provided from the auth system.
This tackles the first access pattern of "Get a build by ID" using the query;
entityType == 'build' && entityId == 'some-random-guid-here'
The query above would be the same for "Get a user by ID" as well, with entityType being set to 'user' instead.
Structuring the Data
Now that we understand how keys work in Dynamo, below is how I decided to structure my build data in Dynamo.
- build
- id: string
- createdOn: int
- createdById: int
- isPrivate: bool
- buildSummaryData: object
Now for the eagle-eyed dev out there, you're probably asking yourself something now: "Why the hell is he using int for createdOn instead of a date?" Well that's because Dynamo doesn't have a Date data type! The way we get around this is to use the epoch time as a timestamp. This would allow me to query builds within a date range provided I convert the timestamp to epoch before querying the date.
Epoch time is an numerical timestamp format that corresponds to a specific date & time. More accurately, it is the number of seconds since midnight on 1/1/1970 UTC.
So we know from the previous section of this article that id corresponds with the SK of the schema, and therefor can be queried directly. The other top-level fields (createdOn, createdById, and isPrivate) will be used for queries too.
I assume you probably have another question at this point: "If we can only query on the PK & SK, how are you going to query on the other fields?"
This is where Indexes come into play.
Indexes in Dynamo
If you want to access your data in different ways that the base schema, indexes help you do this. There are two types of indexes that can be specified in Dynamo:
- Local Secondary Indexes (LSIs) - Use the same PK, but a different SK
- Global Secondary Indexes (GSIs) - Can have a different PK and a different SK
Its worth noting that while GSIs can be created at any time, LSIs need to be specified when the table is first created.
So now lets take a look at the rest of the access patterns specified above and how we can use indexes to address them, along with the queries that will be used.
Get the latest N builds.
LSI Schema:
- PK:
entityType: string - SK:
createdOn: int
Query:
entityType == 'build' && createdOn > '{currentEpochTime}', sort by createdOn descending, get first N records
Get all builds for a user.
LSI Schema:
- PK:
entityType: string - SK:
createdById: int
Query:
entityType == 'build' && createdById == '{userId}'
While none were used initially, I ended up using a GSI for searching, which I'll cover in an upcoming entry.
What About "Get all builds that a user has saved"?
So this is where some creativity comes in. To address this pattern, I didnt actually need another index. Instead, I used a different record structure for bookmarked builds.
- PK:
entityType: string- Always set tobookmarks - SK:
entityId: string- Im actually setting this to theuserIdof the user who saved the build.
Here is the data structure:
- bookmarks
- id: string
- buildSummaries: []object
So you'll notice that there are no real top-level elements being stored simply because I dont need to index any other data. You also might be thinking "Isn't storing the build summary data with the bookmark records going to add duplicate data into the database" The answer is yes, yes it will.
That is one of the tradeoffs of using Dynamo (or most other NoSQL databases). The concept of joins that you'd use in a traditional DB system doesn't really exist. This is why its important to think about access patterns ahead of time.
So while there might be duplicate data, the performance benefits I get from using Dynamo outweigh having to manage that duplicate data. In GuardianForge, there is no way to update builds after they've been created. This means I can confidently know that the build summary data stored in build records should always be consistent with what's stored in the bookmarks records.
About Those Build Summaries
Throughout this article, you'll notice I keep mentioning build summaries instead of build data. As mentioned at the beginning, the bulk of the data for builds is stored in JSON files in S3. I do this because while Dynamo is fast, storing data is generally more expensive than S3.
Looking at GuardianForge, there are what are called "Build Summary Cards" throughout the app. The home page is one example of this.

Those six different blocks are all Build Summary Cards. Any place in the app where I need to load multiple builds will show these because this is the data coming from Dynamo. If you click on any of these, you'll be brought to the build page which has a bunch more info on it. This is accessing the JSON file in S3 (which I'll cover in the next article).
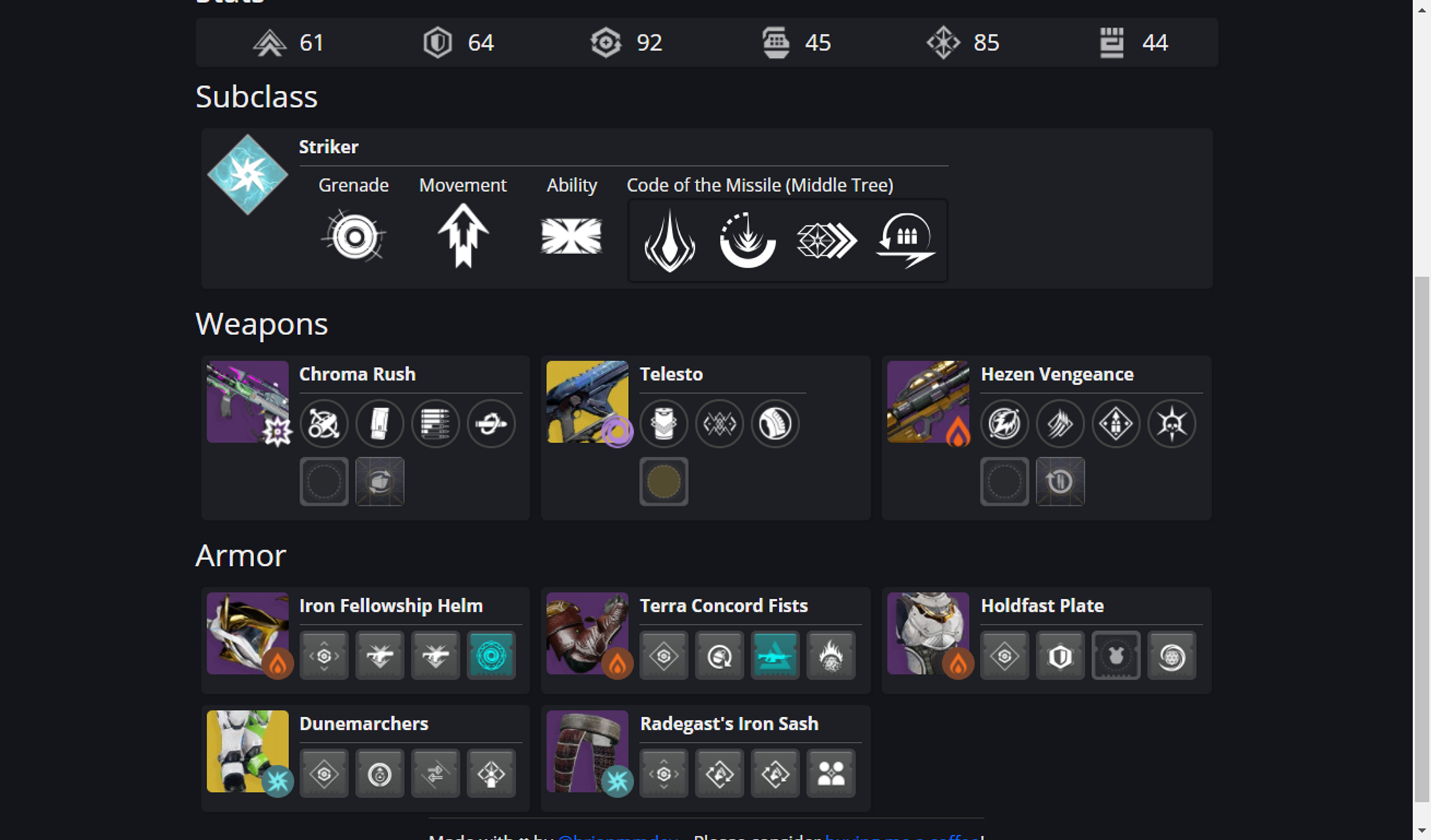
So lets break apart a build card. You'll notice there is a build name, four images, and the users name whos character this was based off of.
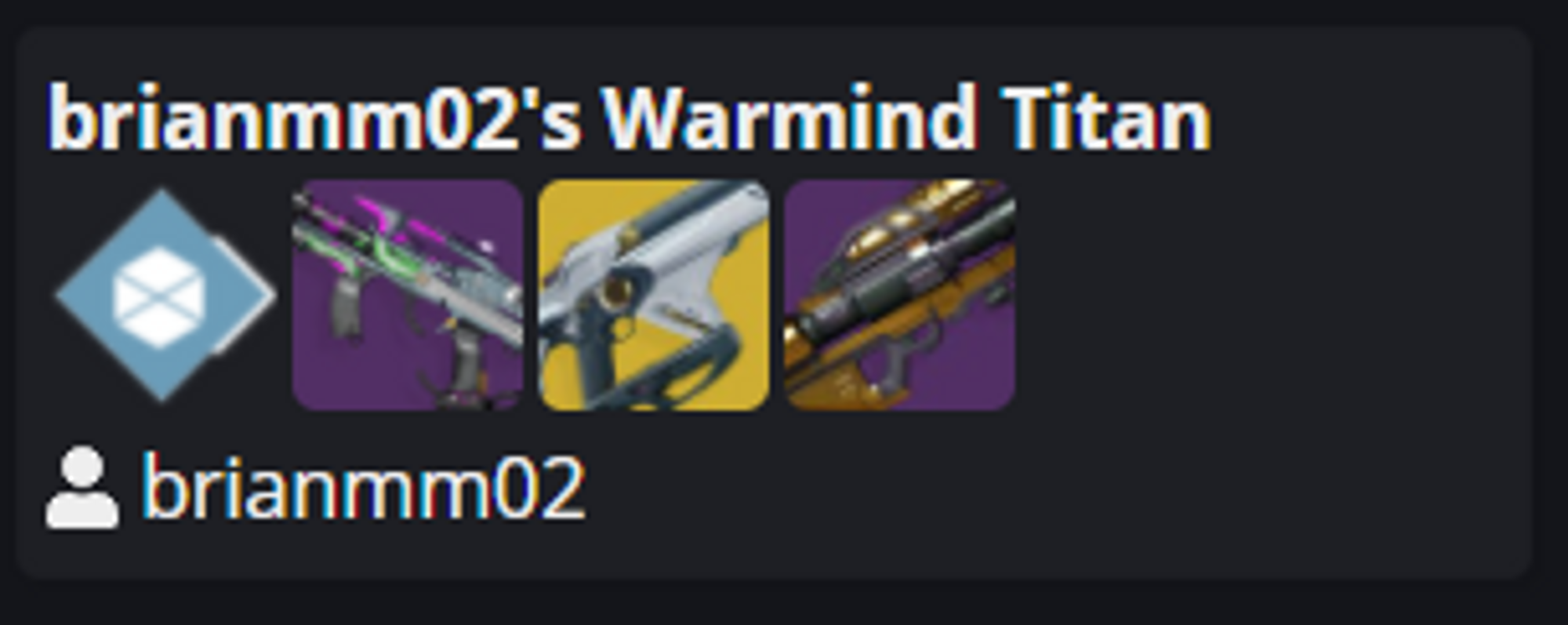
Realistically, that is the only data that needs to be stored in Dynamo. So Im saving cost and increasing performance by storing as little as needed in Dynamo. Comparing what each of these records look like shows what I mean.
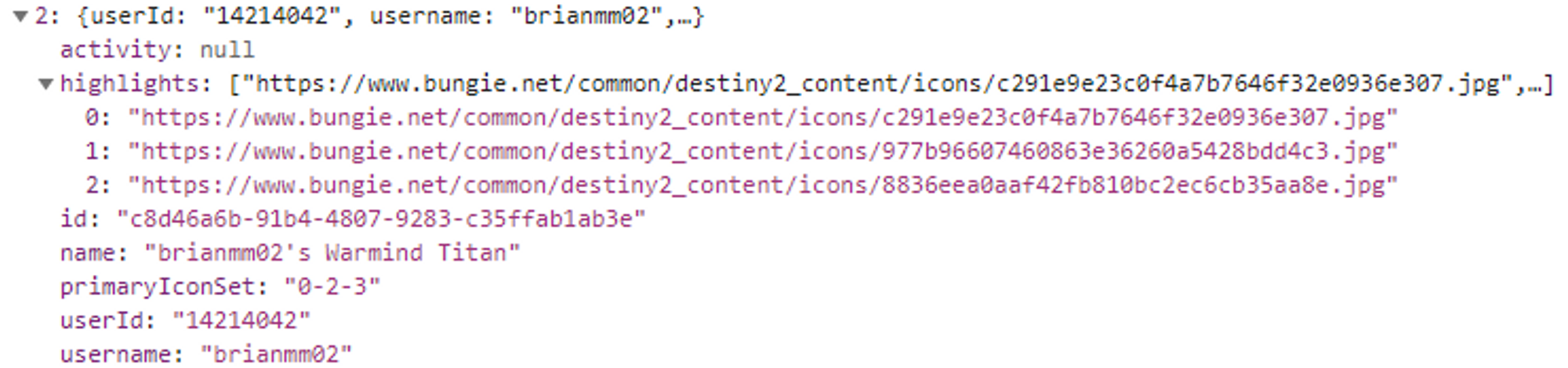
Here is the build summary data that stored for a single build (there is some info that is hidden as well). These records average at about 500 bytes in Dynamo.
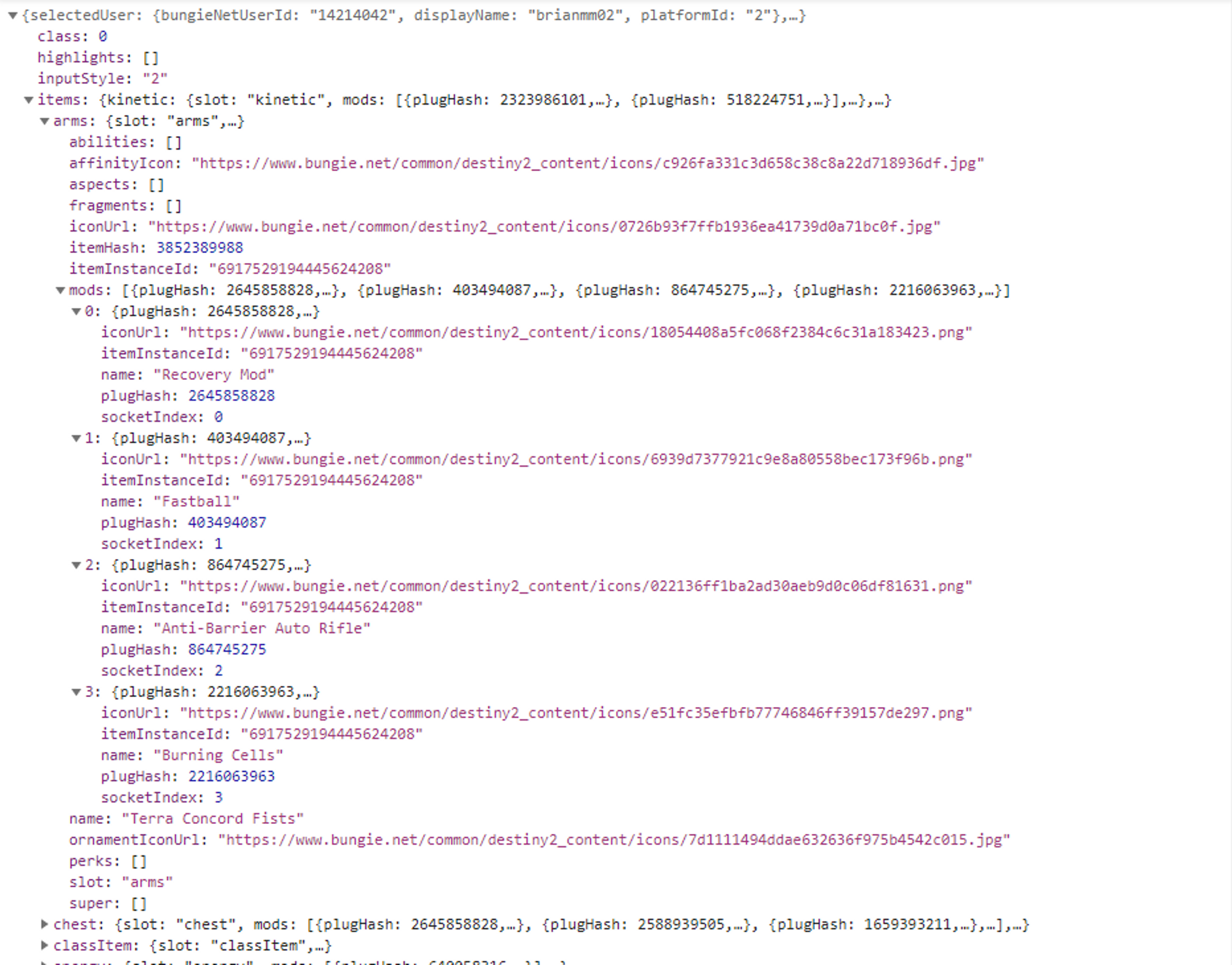
And here is a full build record for that same build from S3. Notice how I have a SINGLE item expanded and the rest of it pretty much goes off the page. This file is about 14KB.
On the surface, 14K doesnt sound huge, and it isn't on its own. But lets see how this scales over time. All values in the spreadsheet below are KB and KB is assumed to be at 1000b instead of 1024b (its just an example).
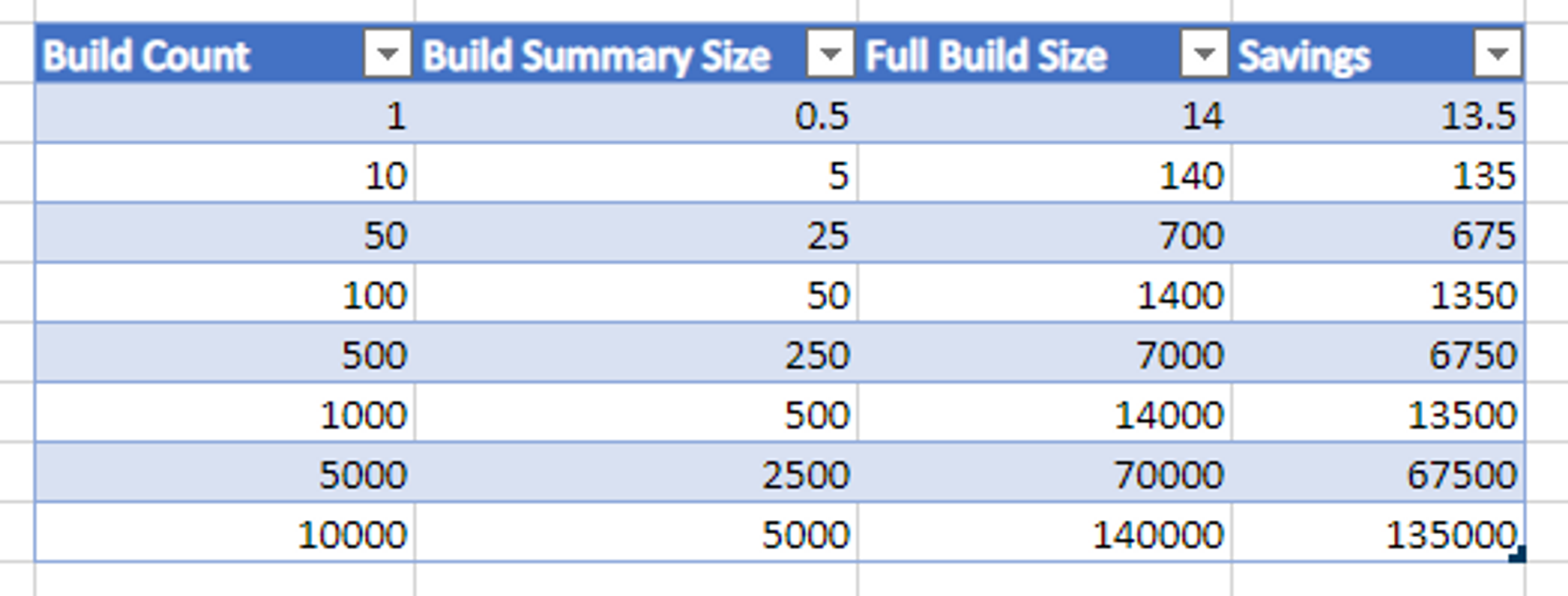
As of this writing, Forge has about 250 builds, which equates to a savings of 3375KB.
Another way to think about this is if I wanted to get a list of all builds in Forge, the response size from the API would be about 125K with the summaries, and about 3.5MB with full builds. That equates to a HUGE performance difference to the user.
Next
In the next article, I'll cover how I setup S3 to access build data and the configuration required there. Got questions? Reach out to me on Twitter @brianmmdev. See you soon!
